Ο κώδικας "Gray" (Gray code) είναι δυαδικό σύστημα αρίθμησης με βασικό χαρακτηριστικό την μεταβολή ενός ψηφίου (bit) σε διαδοχικούς αριθμούς. Σε αντίθεση με την κανονική δυαδική αρίθμηση, κάθε ψηφίο δεν έχει σταθερή "αξία". Στον παρακάτω πίνακα φαίνεται συγκριτικά η αρίθμηση σε δεκαεξαδικό, δυαδικό και gray code:
Κώδικας: Επιλογή όλων
HEX Δυαδικό Gray Code
0 0000 0000
1 0001 0001
2 0010 0011
3 0011 0010
4 0100 0110
5 0101 0111
6 0110 0101
7 0111 0100
8 1000 1100
9 1001 1101
A 1010 1111
B 1011 1110
C 1100 1010
D 1101 1011
E 1110 1001
F 1111 1000Ο κώδικας Gray επινοήθηκε για ελαχιστοποίηση σφάλματος σε αισθητήρια θέσης όπου μια μηχανική ασάφεια μπορεί να "δείχνει" τη διπλανή θέση επειδή άργησε να κλείσει η επαφή ενός ψηφίου. Με τον κανονικό δυαδικό αριθμό, αν η επαφή ενός bit συνδεθεί πριν αποσυνδεθούν όλες οι άλλες, το "παίξιμο" μεταξύ "0111" και "1000" μπορεί να δώσει "1111" δείχνοντας πολύ διαφορετική θέση. Αν υπάρξει αντίστοιχο πρόβλημα στον κώδικα Gray, η αλλαγή αφορά μόνο 1 bit και το σφάλμα θα μείνει μεταξύ δύο διαδοχικών θέσεων. Στο παρακάτω σχήμα φαίνεται αυτή η περίπτωση:
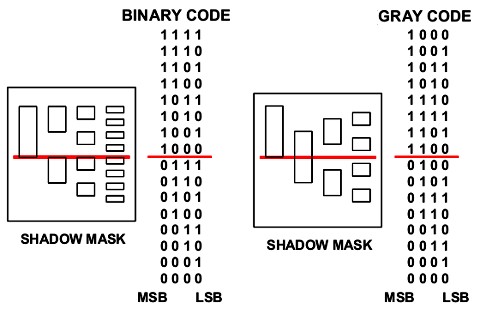
Η κόκκινη γραμμή είναι η δέσμη φωτός του κωδικοποιητή που θα περάσει μέσα από τα κενά της σκιασμένης επιφάνειας και θα "δείξει" τη θέση στα αντίστοιχα δυαδικά ψηφία. Στην κλασική δυαδική κωδικοποίηση, αν περάσει φως από τα κενά της επόμενης θέσης πριν "σβήσει" το πρώτο ψηφίο, ο κωδικοποιητής θα δείξει την αρχή, δηλαδή σφάλμα 50%! Στην κωδικοποίηση Gray, το σφάλμα περιορίζεται +/- 1 θέση, δηλαδή "όσο πρέπει".
Τα ψηφία ενός κωδικοποιητή θέσης κατασκευάζονται από ηλεκτρικές, μαγνητικές ή οπτικές "επαφές".
Για καλύτερη κατανόηση δείχνω πως είναι μέσα ένας κωδικοποιητής απόλυτης θέσης που χρησιμοποιεί κώδικα Gray:

Αξίζει να αναφέρω ότι παραλλαγές του κώδικα Gray χρησιμοποιούνται και στις ψηφιακές επικοινωνίες για μείωση των σφαλμάτων μετάδοσης.
Πως φτιάχνουμε την ακολουθία του κώδικα Gray
Ο μικρότερος κώδικας Gray είναι ... ενός bit και βέβαια είναι ίδιος με τη δυαδική αρίθμηση: 0 1
Για να φτιάξουμε κώδικα με περισσότερα bits, καθρεφτίζουμε τον κώδικα του 1 bit δίπλα του: 0 1 - 1 0
και βάζουμε μπροστά από τα δύο πρώτα το "0" και μπροστά από τα δύο τελευταία το "1": 00 01 - 11 10
Αντίστοιχα, για 3ο bit καθρεφτίζουμε τον κώδικα των 2 bit: 00 01 11 10 - 10 11 01 00
και βάζουμε μπροστά το "0" στα πρώτα και το "1" στα τελευταία: 000 001 011 010 - 110 111 101 100
Δείτε πάλι τον πίνακα παραπάνω...
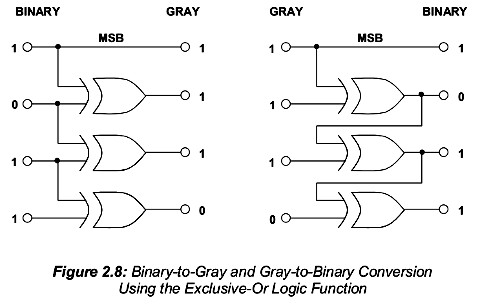
Μετατροπή κώδικα Gray σε δυαδικό και το αντίστροφο
Υπάρχουν διάφοροι λόγοι που χρειαζόμαστε μετατροπή του κώδικα Gray σε δυαδικό (ή το αντίστροφο) όπως η εκτέλεση μαθηματικών πράξεων, συγκρίσεων κλπ. καθώς και η μέτρηση ή απεικόνιση με "συμβατικά" μέσα (βολτόμετρο, A/D, HEX display, ...). Για την μετατροπή μπορούμε να χρησιμοποιήσουμε ένα πίνακα αντιστοίχισης σε μικροεπεξεργαστή, ένα "state machine" με παράλληλη μνήμη ROM ή μια συνδεσμολογία από πύλες XOR: