.
Για το θεωρητικό ζήτημα το οποίο ανακύπτει από την δυνατότητα αλληλεπικάλυψης των διαστημάτων αντίστασης σε μια Standard E Series, με την μη-κενή τομή τους να αποτελεί διάστημα αντιστάσεων που είναι συνημμένες σε δύο διαφορετικές, διαδοχικές στην E Series, ονομαστικές τιμές αντίστασης, ξεκινάμε αναζητώντας ένα κατάλληλο μέρος από το διαφωτιστικό Σχήμα του ARTol Lex Tollenaar για την Standard E12 Series, που έχει Tolerance ±10, στο επίμαχο λήμμα στην wikidedia:
https://en.wikipedia.org/wiki/File:E12_series_10%25_tolerance.png
το οποίο και εντοπίσαμε πλησίον του δεξιού τέλους του εν λόγω σχήματος, όπου άνω δεξιά και για τις τρεις διαδοχικές ονομαστικές τιμές αντίστασης των 56 Ω, 68 Ω , και 82 Ω, το διάστημα αντιστάσεων της ενδιάμεσης ονομαστικής τιμής των 68 Ω αλληλεπικαλύπτεται με τα εκατέρωθέν του διαστήματα αντιστάσεων των 56 Ω και 82 Ω, οπότε, αποσπάσαμε το κομμάτι αυτό από το Σχήμα, το τακτοποιήσαμε κατάλληλα, σημειώσαμε επάνω του με μπλε χρώμα τις δύο αυτές κτυπητές αλληλεπικαλύψεις, τις οποίες και προβάλαμε στην συνέχεια επάνω στον αριστερό κατακόρυφο άξονα τιμών αντίστασης, όπου και φαίνεται πια για τα καλά, και αμέσως και με το μάτι, πως δεν είναι και τόσο αμελητέες:
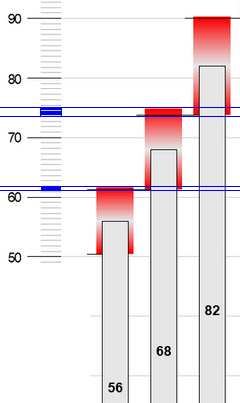
αφού η κάτω αλληλεπικάλυψη δίνει ένα μη-κενό διάστημα εύρους περίπου ~1 Ω και η άνω αλληλεπικάλυψη άλλο ένα μη-κενό διάστημα εύρους περίπου ~2 Ω , δύο εύρη που επακριβώς είναι περίπου τα μισά αυτών με το μάτι:
56 + 5.6 = 61.6 : Ω
68 - 6.8 = 61.2 : Ω
0.4 : Ω
κάτω αλληλεπικάλυψη
με
προηγούμενο διάστημα αντίστασης
και
68 + 6.8 = 74.8 : Ω
82 - 8.2 = 73.8 : Ω
1.0 : Ω
άνω αλληλεπικάλυψη
με
επόμενο διάστημα αντίστασης
Αυτό σημαίνει ότι το Standard E12 επιτρέπει γενικώς, μεταξύ και των άλλων αναλόγων περιπτώσεων που φαίνονται στο Σχήμα της wikipedia, να υπάρχουν ειδικώς, όπως φαίνεται στο ως άνω απόσπασμα του ιδίου Σχήματος, τιμές αντίστασης εύρους 0.4 Ω που είναι συνημμένες σε δύο διαφορετικούς αντιστάτες με διαφορετικές ονομαστικές τιμές αντίστασης 56 Ω και 68 Ω , καθώς και να υπάρχουν τιμές αντίστασης εύρους 1.0 Ω που είναι συνημμένες σε δύο δύο διαφορετικούς αντιστάτες με διαφορετικές ονομαστικές τιμές αντίστασης 68 Ω και και 82 Ω αντιστοίχως.
Περιθωριακό μεν αλλά δυσάρεστο.
Την ύπαρξη αυτού του ζητήματος παραδέχεται σαφώς και το ίδιο το Standard (SAMPLE, p.8):
"A sequential range of components is usually established in a way that
a tolerance range of any given value, i.e. the range defined by that given value minus and plus the given tolerance, does
not significantly overlap with the tolerance range of the next succeeding value. This consideration suggests a fixed relationship between the tolerance and the progression ratio of any range of components."
αν και με την αρνητική του διατύπωση επιχειρεί να το υποβαθμίσει : "does not significantly".
Ενώ προσέχουμε ιδιαίτερα στο σημείο αυτό και την ορολογία που χρησιμοποιεί το Standard:
Tolerance είναι η τιμή που ορίζει το συμμετρικό διάστημα της Tolerance μιας δοθείσης τιμής και ΌΧΙ όπως σαφώς εμείς θεωρούμε το δοθέν συμμετρικό διάστημα της αντίστασης που είναι αναπόσπαστα συνημμένο την ονομαστική της τιμή.
Λεπτομέρειες; Τέλος πάντων. Καταλάβαμε πως λειτουργούνε εκεί μέσα.
Εν πάση περιπτώσει όμως μετά από αυτά αναρωτιέται κανείς ευλόγως αν πέραν από τις επιδιώξεις της παραγωγής είναι δυνατόν να επιδιωχθεί η περίπτωση εντοπισμού μιας τιμής για την Tolerance που θα επιτρέπει την επαφή των των γειτονικών διαστημάτων αντίστασης, ήτοι την ευρύτερη δυνατή περίπτωση της ΜΗ-αλληλεπικάλυψής τους.
Κι αυτό ήταν όλο κι όλο αυτό που "κρυβόταν" μέχρι τώρα στην "μυστηριώδη" διατύπωση "Calculated Tolerance" της wikipedia και μας οδήγησε στην "ομολογία" του μηνύματός μας : "Κάναμε Τρεις Φορές Λάθος Μέχρι να Επαληθεύσουμε τον "Μυστηριώδη" Χαρακτηρισμό "Calculated Tolerance" της Wikipedia" - που σαν να μου φαίνεται πως ενώ το βρίσκει η Αναζήτηση εν τούτοις αυτό,
ΤΟ ΤΟΣΟ ΠΟΛΥ ΑΠΟΚΑΛΥΠΤΙΚΟ ΓΙΑ ΤΟΝ ΤΡΟΠΟ ΠΟΥ ΔΙΕΞΑΓΕΤΑΙ Η ΑΝΑΖΗΤΗΣΗ ΤΗΣ ΕΡΕΥΝΑΣ
μήνυμα δεν υπάρχει πια! Φαίνεται πως σβήσε-γράψε και πάνε-έλα από τις Πρόχειρες Σημειώσεις χάθηκε κάπου στον δρόμο... Θα το αναζητήσω στον υπολογιστή μου και θα το αποκαταστήσω εκ νέου εδώ.
Λοιπόν.
Για να απαντηθεί το ζήτημα αυτό Εργασθήκαμε αρχικά προσθέτοντας όλα τα μήκη των διαστημάτων που εμπλέκονται, προσθαφαιρέσαμε τον πρώτο και τον τελευταίο όρο, χρησιμοποιήσαμε τον τύπο για το Άθροισμα όλων των όρων μιας Γεωμετρικής Προόδου, κι όταν επιτέλους φθάσαμε στο "αμείλικτο" : ) για την Tolerance αποτέλεσμα : (ω - 1) / (ω + 1) , ήταν μόλις λίγο χαρήκαμε όταν καταλάβαμε πως έπρεπε να βρούμε έναν απλούστερο τρόπο να το δείξουμε, οπότε και προέκυψε ο ακόλουθος που πιο απλό εμείς την στιγμή αυτή δεν βλέπουμε:
1 Έστω δύο θετικοί αριθμοί a =/= b τέτοιοι ώστε 0 < a < b
(στο τέλος θα γίνουν δύο διαδοχικές αντιστάσεις από μια E Series):
.------|--------------------|
0 a b
2 Αυτοί απέχουν μεταξύ τους κατά απόσταση b-a
(θα γίνει το γεωμετρικό βήμα μιας E Series):
.------|--------------------|
0 b-a
3 Για κάθε άλλο χ μεταξύ τους έχουμε a < x < b
(θα γίνει το ζητούμενο σημείο επαφής δύο γειτονικών διαστημάτων αντίστασης e Series):
x
.------|-------|------------|
0 a b
4 Οι αποστάσεις του χ από τα a και b είναι
(θα γίνουν τα μήκη των γειτονικών διαστημάτων αντίστασης που εφάπτονται):
.------|-------|------------|
0 x-a b-x
5 Ερώτηση: Υπάρχει k τέτοιο ώστε χ-a = k.a και b-x = k.b ;
(υπάρχει και θα γίνει η Κοινή τιμή της Tolerance για την E Series):
k.a k.b
.------|-------|------------|
0 x-a b-x
6 Υπάρχει, αν και μόνον αν ισχύει
(η απόσταση των δύο διαδοχικών ονομαστικών τιμών είναι ίση με το άθροισμα των μηκών των δύο εφαπρομένων διαστημάτων αντίστασής τους):
k.a + k.b = x-a + b-x = b-a
7 Κι αυτό είναι το k
(θα γίνει η ζητούμενη Κοινή τιμή της Tolerance για την E Series):
+===========+
| b-a |
| k = ----- |
| b+a |
+-----------+
Και να η Εφαρμογή της:
Έστω E Series με πρώτο όρο α και λόγο ω > 1 , δηλαδή αύξουσα (π.χ. Ε3 με α = 1 και ω = 3√10).
Έχουμε για τον ν αντιστάτη της Ε3, όπου 0 =< ν < 3:
a = α.ω^ν
b = α.ω^(ν+1)
Άρα, για την Tolerance k της E Series:
α.ω^(ν+1) - α.ω^ν ω - 1
k = ----------------------- = ------
α.ω^(ν+1) + α.ω^ν ω + 1
και σημειώνουμε ότι αφού ω > 1 και ω - 1 < ω + 1 προκύπτει να είναι 0 < k < 1
Και να η άμεση Εφαρμογή της ("calculated tolerance" στην wikipedia:
3√10 - 1 / 3√10 + 1 = ~0.3660 ή 36.60%
.
Παρατήρηση - Που ως καλύτερη την αφήσαμε για το τέλος
Στο βήμα 5 χ-a = k.a και b-x = k.b έχουμε "κρυμμένη" την Tolerance η οποία εξ ορισμού είναι
(x-a)/a = k = (b-x)/b
ήτοι
(χ - α.ω^ν) / (α.ω^ν) = Tolerance = (α.ω^(ν+1) - χ) / (α.ω^(ν+1)
όπου βεβαίως η τιμή της αντίστασης επαφής των διαστημάτων χ εξαρτάται από τον όρο όπου την θεωρούμε.
Τώρα ανοίγονται από εδώ και άλλα θέματα το κυριότερο από τα οποία είναι -κατά την γνώμη μας- η εύρεση του λόγου ω της όποιας
εμείς θέλουμε -λέμε τώρα- να "κατασκευάσουμε" "δικής μας" : ) σειράς E:
Γράφουμε στην θέση του k το k / 1 και έχουμε:
k / 1 = (ω - 1) / (ω + 1)
Μετά προσθέτουμε παρονομαστές συν αριθμητές, αφαιρούμε παρονομαστές μείον αριθμητές (k < 1) και διαιρούμε κατά μέλη, οπότε η αναλογία διατηρείται:
(1 + k) / (1 - k) = (ω + 1 + ω - 1) / (ω + 1 - ω - (- 1)) = 2.ω / 2 = ω
Οπότε, δίνουμε το k που επιδιώκουμε ως κατασκευαστές : ) και βρίσκουμε το ω της σειράς.
Παράδειγμα : Επειδή η κατασκευαστική μας δυνατότητα είναι αντιστάτες με ανοχή 50% ή 0.5 -είπαμε : εμείς είμαστε οι κατασκευαστές- θα βγάλουμε μια δική μας σειρά "e" οι αντιστάτες της οποίας θα είναι όροι γεωμετρικής προόδου με λόγο
ω = (1 + 0.5) / (1 - 0.5 ) = 1.5 / 0.5 = 3
Κι από που θα ξεκινήσουμε; Πόσο δηλαδή θα είναι το α της e series μας;
Χμ... Κι εδώ είναι που αρχίζουν τα "κατασκευαστικά δύσκολα"...
Αν επιχειρήσουμε να ακολουθήσουμε την κατασκευαστική πεπατημένη που ξέρουμε πως θέλει αλλά μπορούμε μόνον να υποπτευόμαστε και να πιθανολογούμε για ποιον λόγο το θέλει, τότε αρχίζουμε να παίζουμε με τα significant digits και τις decades.
Αν λοιπόν αποφασίσουμε να ψάξουμε για ίδιο πλήθος αντιστατών ανά decade, ας πούμε Λ
-
"decade" = "δεκάδα" (Νέα Γλώσσα) = "δεκάς" (Αρχαία-Καθαρεύουσα-Νέα Γλώσσα)
Διάστημα τιμών με λόγο άνω-προς-κάτω άκρο = 10
-
και διαλέξουμε να βγάζουμε αντιστάτες ξεκινώντας από τα 10,000 Ω τότε θα πρέπει να έχουμε για το πλήθος Λ
Λ√10 = 3
10^(1/Λ) = 3
(1/Λ) = log(3)
Λ = 1/log(3) ~= 1/0.477 ~= 2.095...
που είναι αριθμός με μη-μηδενικό δεκαδικό μέρος άρα δεν υπάρχει ως πλήθος.
= Οπότε;
- Προσεγγίσεις οι Αναπόφευκτες. Στον πλησιέστερο φυσικό. Που είναι το 2:
"Πες" Λ = 2 και "Ξέχνα το".
Πάμε με την πρόοδο (Θ = Θεωρητικά , Π = Πρακτικά):
Θ 10,000 Ω - Π 10,000 Ω
Θ 30,000 Ω - Π 31,663 Ω
Θ 90,000 Ω - Π 100,000 Ω
κ.λπ.
Τις κατασκευάσαμε και πάμε για βάψιμο.
Τόμπολα!
Η Π 31,663 της "e" έχει 5 significant digits κι αν την θέλουμε αναβαθμισμένη, σε επίσημα στανταρισμένη έκδοση, τότε δεν βάφεται!
Το Standard το λέει καθαρά (SAMPLE, p.8):
"... all established and practical coding and marking systems are limited to a resolution of three significant digits and thus pose a constraint to the use of numeric values with more than three significant digits."
: )
.
- Λίγο Αργότερα - Βρέθηκε και μια version του μηνύματος, που λέγαμε, κι από ότι βλέπω μάλλον ήπια ως προς τον αυτοχαρακτηρισμό μας, οπότε συμπληρώνω από μνήμης ενώ αντιγράφω από το screen capture που έχω κρατήσει:
Κάναμε Τρεις Φορές Λάθος Μέχρι να Επαληθεύσουμε τον "Μυστηριώδη Χαρακτηρισμό "Calculated Tolerance" της Wikipedia
09 Feb 2022, 07:27
.
... και τον αποκαταστήσαμε στο λήμμα:
https://en.wikipedia.org/wiki/E_series_of_preferred_numbers#E3
ενώ και πάλι δεν θα σβήσουμε αλλά μόνον θα διαγράψουμε τους -στην περίπτωση αυτή, και παρά την αοριστολογία της- χαρακτηρισμούς μας που ως αποδείξαμε ήταν εμπαθείς.
- Η Απόδειξη Ακολουθεί Οσονούπω -
Και από μνήμης:
Καλά Να Πάθουμε! Να Μάθουμε Να Μην Είμαστε Προκατειλημμένοι Επειδή Μερικοί Εκεί Μέσα Είναι - κάτι, αλλά άλλο δεν θυμάμαι τι...
: )
.