.
Από τα προηγούμενα κατεβατά των Τριάδων (ΘΕΤΙΚΩΝ) Αριθμητικών
Διαφορών Διαδοχικών (Αμέσως Μεγαλύτερη ΜΕΙΟΝ Μόλις Μικρότερη)
Αντιστάσεων Κ Ρ Ι Ν Α Μ Ε πως, παραλείποντας είτε τον Αντιστάτη 2'
είτε το 3', ΟΛΕΣ οι Διαφορές ΤΑΙΡΙΑΖΟΥΝ ΜΊΑ-ΜΊΑ.
Για να δούμε -κυριολεκτικά- αν και κατά πόσον ΤΑΙΡΙΑΖΟΥΝ πράγματι
ΚΑΙ ΕΝ ΣΥΝΟΛΩ, οι εν λόγω διαφορές, σκεφθήκαμε να συγκρίνουμε
τις Διαφορές αυτές ανά Δύο Πολύμετρα, ξεκινώντας με τα
HP34410A-GE και HP34401Α-45.
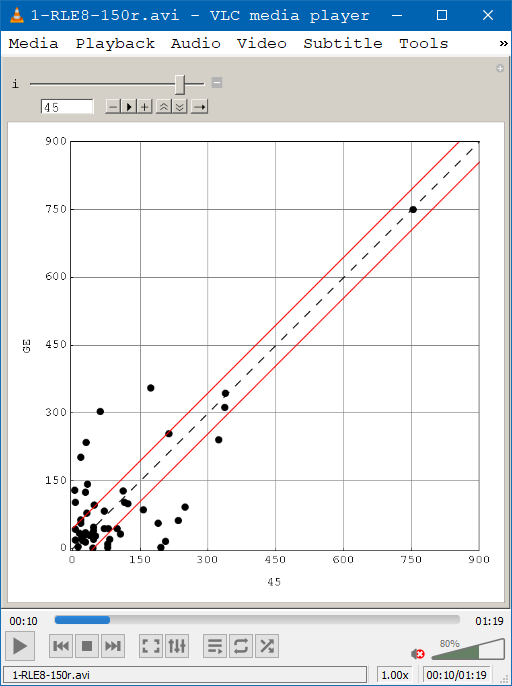
Συγκεκριμένα, βάλαμε την Mathematica να ζωγραφίσει ένα καρτεσιανό
διάγραμμα και να τοποθετήσει επάνω του σαν σημεία τα 49 ζεύγη των εν
λόγω Αριθμητικών Διαφορών:
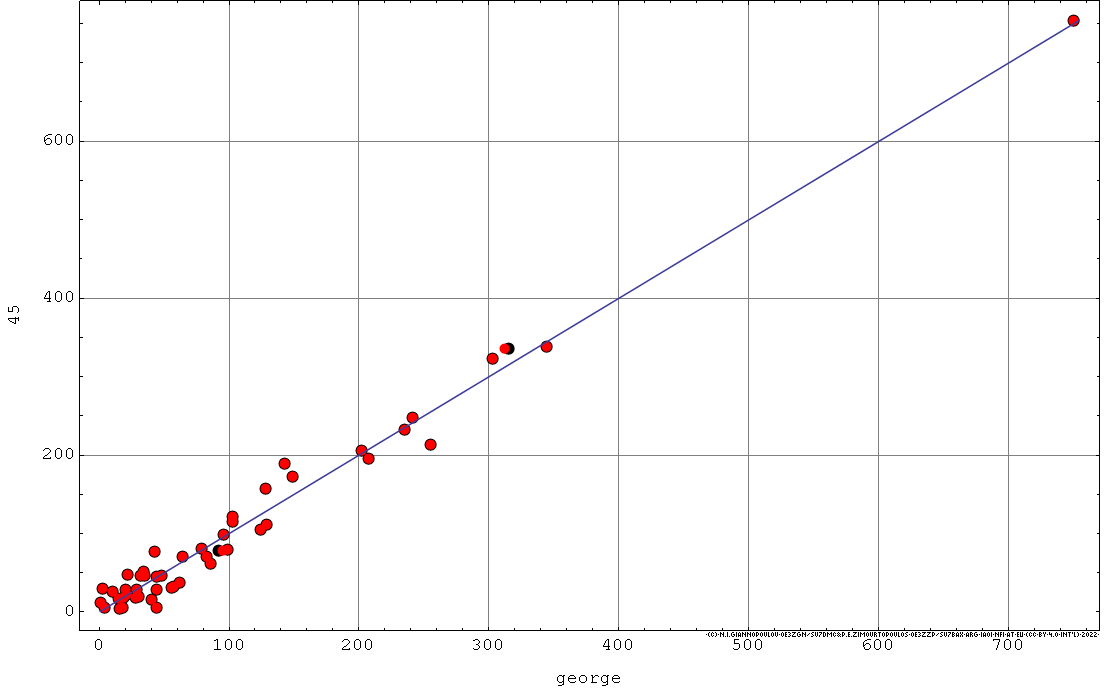
- Και τι βλέπουμε;
- Μαύρα κυκλάκια, που τοποθετήθηκαν πρώτα -παραλείποντας τον 2'- και
Κόκκινα κυκλάκια, που τοποθετήθηκαν ύστερα -παραλείποντας τον 3'-,
να σκεπάζουν σχεδόν πλήρως σχεδόν όλα τα μαύρα κυκλάκια πλην δύο
από αυτά - ως βεβαίως ανεμένετο, αφού μαύρα και κόκκινα κυκλάκια
προέρχονται από 47 ίδια ζεύγη Διαφορών πλην των δύο διαφορετικών
λόγω της διαφορετικής παραλείψεως.
- Και τι συμπεραίνουμε;
- Πως ΌΛΑ τα κυκλάκια των Ζευγών των Διαφορών, και τα 49, βρίσκονται
είτε πλησίον είτε επάνω στην Γενική Θεωρητική Διαγώνιο της Ταυτότητας,
που εδώ είναι ειδικά η Θεωρητική Ταυτότητα των Διαφορών.
- Άρα ΚΡΙΝΟΥΜΕ πως ΝΑΙ, ΠΡΑΓΜΑΤΙ, οι Αντίστοιχες Διαφορές ΔΕΙΧΝΟΥΝ
ΤΑΙΡΙΑΣΤΕΣ. Οπότε, αφού ΤΑΙΡΙΑΖΟΥΝ, ΦΑΙΝΕΤΑΙ να λείπει ο 2' ή ο 3'.
.